neuroscience-ai-reading-course

Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks

Created: Jul 10, 2020 3:20 PM

Description: Train a model on some tasks such that when a new task is presented, it only needs to run a few gradient steps on a few training samples to generalize well on the new task.

Materials: https://arxiv.org/pdf/1703.03400.pdf

Status: Done reading

To do:

• Read about on-policy gradient methods (how to approximate gradients on expectation of rewards?)
• Read prior work (given in introduction and related work)

Key words

Model-agnostic: Not knowing the details of the model. Independent of the model used.

Meta-Learning: Learning how to learn. Train a model on a variety of tasks such that the model can learn to generalize well on the new task even when exposed to very little training data.

Few-shot learning: Training a model on a few instances ($K$ instances in the case of $K$-shot learning) from the dataset (as opposed to training on a large number of instances).

Why is Meta-Learning a challenge?

1. The model may chose to discard its prior experience and just overfit on the new task
2. The learning process shouldn’t be specific to certain tasks as the new task can be of any type

What does the paper propose?

A meta-learning algorithm that can be applied to any learning algorithm and any model trained using gradient descent.

Key Idea

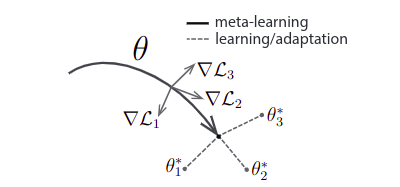
Train the model already to a point that when a new task is presented, it only needs to “finetune”, i.e., take a small number of gradient steps to achieve good performance on the new task. Hence, we want to train the model to the point from which it can adapt “fast” to any new task.

How is this different from prior work?

1. It does not learn an update function or a learning rule
2. It does not increase the number of parameters
3. It does not place constraints on model architecture
4. It can be used with any model and any kind of loss function. Note that the loss function needs to be differentiable. If it is not, then it needs to be either reduced to or approximated by a differentiable form.

Intuition

1. From a feature learning standpoint: Find an internal representation that is broadly suitable for many tasks. Basically, if this representation is broad enough, it can be used to finetune a little and reach optima for several tasks.
2. From a dynamical systems standpoint: Maximize the sensitivity of loss functions of new tasks with respect to parameters. Hence, this high sensitivity causes losses to improve by a large amount when small local changes are made to the parameters.

Defining a task

Let $T$ denote a generic task. Then it can be represented as follows:

$$T = \{L(x_{1}, a_{1}, ..., x_{H}, a_{H}), q(x_{1}), q(x_{t+1} | x_{t}, a_{t}), H\}$$

where $L$ is the loss function corresponding to the task, $q(x1)$ is a distribution over initial observations, $q(x_{t+1}

x_{t}, a_{t})$ is a transition distribution and $H$ is the horizon (episode length).

For supervised learning tasks, $H = 1$ and the task definition can be simplified as follows:

$$T = \{L, q(x), q(y | x)\}$$

Meta-Learning Problem Setup

You have a distribution of tasks $p(T)$. There are two phases of training: meta-training phase (where the meta-learning parameters are optimized) and the adaptation phase (where your model adapts to a new task). The tasks are also divided into meta-training and meta-testing tasks.

Meta Training: Pick a task $T_{i}$ from $p(T)$. Take $K$ samples from the dataset of $T_{i}$. Train the model $f$ on the $K$ samples using the loss function $L_{i}$. Now take a few testing samples for $T_{i}$ and test the model $f$ on these samples. Update the parameters of $f$ based on the loss generated over the test samples. Repeat this for how many ever meta-training tasks.

Adaptation: Pick a meta-testing task $T_{i}$. Take $K$ samples from this task and update the model $f$. Now test the model on testing samples from $T_{i}$. This gives the meta-performance of the final model.

The MAML Algorithm

Let the parameters of the model be denoted by $\theta$. Sample some tasks from the task distribution. Take $K$ samples of each task and train the model $f$ using gradient descent on the initial parameters $\theta$.

For each task $T_{i}$, the update will be of the following form:

$$\theta'_{i} = \theta - \alpha \nabla_{\theta}L_{T_{i}}(f_{\theta})$$

After doing this for all the tasks, update the parameters $\theta$ using the following update rule:

$$\theta = \theta - \beta\nabla_{\theta}\sum_{T_{i} \sim p(T)} L_{T_{i}}(f_{\theta'_{i}})$$

The algorithm can be summarized as follows:

Experiments

MAML was tested against the following tasks against a pre-trained network and a network with random initialization. The performance was also compared to other approaches to the problems wherever applicable.

1. Supervised few-shot learning

   The MAML algorithm for supervised few-shot learning is as follows:

   

   a. Few-shot regression:

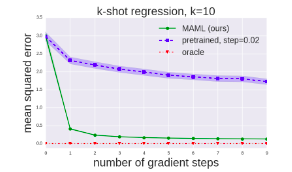
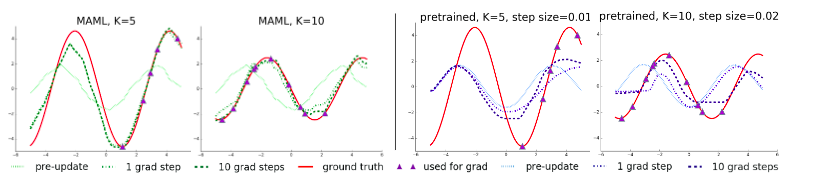
   Tested on Sinusoidal wave regression. The task distribution consisted of sine waves of different amplitudes and phase differences. The model trained using MAML could rightly model the part of sine wave whose data points were not presented.

   b. Few-shot classification:

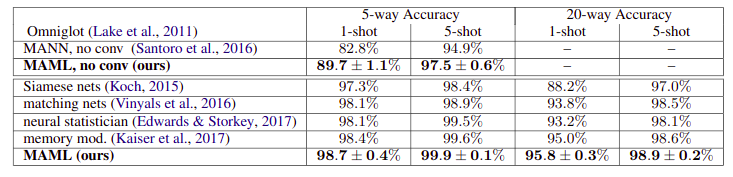
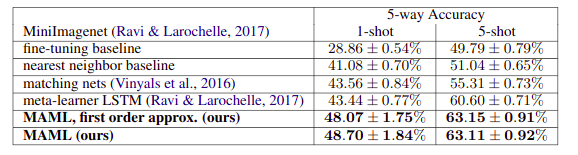
   Tested on Omniglot and MiniImagenet image recognition tasks. Achieved state-of-the-art results even when using a first-order approximation of the double-derivative.

2. Meta-Reinforcement Learning (using policy gradients)

   The MAML algorithm for Meta-RL is as follows:

   

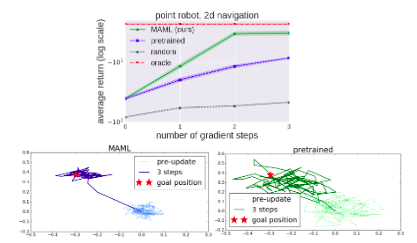
   Tested on 2-D Navigation and Locomotion tasks. Outperformed pre-training and random initialization even when adaptation was performed using a single gradient step.

Results

MAML achieved state-of-the-art performance in supervised few-shot learning tasks and meta-reinforcement learning tasks.

1. Few-shot regression

   

   

2. Few-shot classification

   

   

3. Meta-Reinforcement Learning